
量子コンピュータに関して専門知識がなくても理解できるようになることを目指した本連載。第3話ではついに量子ビットや量子ゲートを学びました。新しい概念も登場し、理解に時間がかかった方もいるかもしれません。
第4話では、量子回路と量子ゲートについて具体的に学んでいきます。馴染みのあるような回路図も登場し、エンジニアなら気になる量子プログラミングに近づいてきました。計算例も併記しましたので、詳しく学びたい方はゆっくり繰り返し読んで理解してみてください。
最後のコラムでは注目技術の影で量子コンピュータを支えている技術について、解説いただきました。これを抑えておくと量子コンピュータを「分かっている人」になれるはず。
【筆者】束野 仁政さん
量子コンピュータ・プログラマ。学生時代に数学を専攻したのち、ソフトウェア・エンジニアを経て、現在は研究機関にて量子コンピュータの仕事をしている。量子コンピュータの面白さを多くの人に広めたいと思い、雑誌記事や同人誌の執筆、勉強会での発表等を行う。著書は「Elasticsearch NEXT STEP」(インプレスR&D)・Twitterアカウント(https://twitter.com/snuffkin)
■免責
本連載は情報の提供のみを目的としています。
本連載の内容を実行・適用・運用したことで何が起きようとも、それは実行・適用・運用した人自身の責任であり、著者や関係者はいかなる責任も負いません。
■商標
本連載に登場するシステム名や製品名は、関係各社の商標または登録商標です。 また本書では、™、®、© などのマークは省略しています。
第3話までに、量子状態、ユニタリ発展、測定について学びました。今回は、それらを組み合わせて量子回路を作る方法を学びます。具体的な計算を通じて、1量子ビットと2量子ビットの代表的な量子ゲートを理解します。行列の計算が多く登場しますので、少しずつ慣れながら進みましょう。
量子ゲートと量子回路
古典コンピュータの計算ついて説明するとき、回路を図示した回路図がよく使われます。たとえば、図1.1のような回路図です。

▲図1.1:古典ビットの回路図
このようにAND,OR,NOTなどのゲート(素子)を組み合わせたものが、回路です。回路の左からデータを入力し、ゲートで計算した結果を右から出力します。1本の線には1ビットのデータが流れます。
図1.1の場合は、入力は2ビット、出力も2ビットです。
量子コンピュータの場合も、量子状態を操作する量子ゲート(量子素子、quantum gate)を組み合わせて量子回路(quantum circuit)を作成します。この量子回路に量子状態を入力することで、計算が行われます。量子状態は初期状態$\Ket{0}$ からはじまり、量子ゲートを使ってユニタリ発展し、測定して実行結果を量子回路から取り出します。ユニタリ発展を数学の言葉で表現したものがユニタリ行列であるため、量子ゲートとユニタリ行列を同一視して話を進めます。
また、量子回路の図の記法は、いくつか流儀があります。文献によってはこの連載で説明する記法と異なるため、注意してください。
基本の量子ゲート
代表的な量子ゲートについて説明します。それぞれの量子ゲートがどのように動作するか分かるように、具体的な計算例も明記します。このあたりの手触りを感じたい方は、実際に計算例を追ってみましょう。

▲表1:代表的な量子ゲートまとめ
■重ね合わせ状態を作る「アダマールゲート」
まずは、数学者のアダマールさんに由来するアダマール行列(Hadamard matrix)
アダマール行列$H$を使うと、$\Ket{0}$や$\Ket{1}$から重ね合わせ状態を作ることができます。
逆に$\Superposition, \SuperpositionZ$という重ね合わせ状態から、
重ね合わせ状態を作り出して計算する量子アルゴリズムは非常に多いため、$H$は大活躍する量子ゲートのひとつです。
量子回路を書くときは、図1.2のように表記します。左から量子状態を入力し、ユニタリ発展したあとの量子状態を右に出力します。

▲図1.2:アダマール行列の量子回路
アダマール行列$H$がユニタリ行列であることを確認しましょう。
$H^{\dagger}= \FracTwo\TwoTwo{1}{1}{1}{-1}$なので、
$\begin{array}{ll} H^{\dagger}H &= \FracTwo\TwoTwo{1}{1}{1}{-1} \cdot \FracTwo\TwoTwo{1}{1}{1}{-1} \\[10pt] &= \frac{1}{2}\TwoTwo{2}{0}{0}{2} = \TwoTwo{1}{0}{0}{1} = I\end{array}$
となります。これで、$H$がユニタリ行列であることを確認できました。
$H$により、量子状態$\Ket{0}, \Ket{1}, \Superposition, \SuperpositionZ$は次のように変化します。
■NOTの役割を果たす「Xゲート」
次は物理学者のパウリさんに由来するパウリ行列(Pauli matrices)です。
パウリ行列にはいくつか種類がありますが、今後よく利用することになる$X$と$Z$を紹介します。この連載では、大文字の$X$や$Z$は変数としては使わず、パウリ行列を表します。
まずは、パウリ行列$X$です。
パウリ行列$X$を使うと$\Ket{0}$が$\Ket{1}$に、$\Ket{1}$が$\Ket{0}$に変化します。これにより、ビット反転(bit flip)を実現できます。古典ゲートでいうとNOTに相当します。また、$\Superposition$は、$\Ket{0}$と$\Ket{1}$が反転しても$\Superposition$のままです。
$\SuperpositionZ$は、$\Ket{0}$と$\Ket{1}$が反転すると、$-1$倍した$-\SuperpositionZ$に変化します。
量子回路を書くときは、図1.3のように表記します。

▲図1.3:パウリ行列Xの量子回路
パウリ行列Xがユニタリ行列であることを確認しましょう。
$X^{\dagger}= \TwoTwo{0}{1}{1}{0}$なので、
$\begin{array}{ll} X^{\dagger}X &= \TwoTwo{0}{1}{1}{0} \TwoTwo{0}{1}{1}{0} \\[10pt] &= \TwoTwo{1}{0}{0}{1} = I \end{array}$
となります。これで、$X$がユニタリ行列であることを確認できました。
$X$により、量子状態$\Ket{0}, \Ket{1}, \Superposition, \SuperpositionZ$は次のように変化します。
■位相反転させる「Zゲート」
次はパウリ行列$Z$です。
$\begin{array}{l} Z := \TwoTwo{1}{0}{0}{-1} \end{array}$
パウリ行列$Z$は$\Ket{0}$を変化させませんが、$\Ket{1}$の係数の符号を反転させます。 これを、位相反転(phase flip)と言います。量子回路を書くときは、図1.4のように表記します。

▲図1.4:パウリ行列Zの量子回路
パウリ行列Zがユニタリ行列であることを確認しましょう。
$Z^{\dagger}= \TwoTwo{1}{0}{0}{-1}$なので、
$\begin{array}{ll} Z^{\dagger}Z &= \TwoTwo{1}{0}{0}{-1} \TwoTwo{1}{0}{0}{-1}\\[10pt] &= \TwoTwo{1}{0}{0}{1} = I \end{array}$
となります。これで、$Z$がユニタリ行列であることを確認できました。
パウリ行列$Z$により、量子状態$\Ket{0}, \Ket{1}, \Superposition, \SuperpositionZ$は次のように変化します。
■「位相」とは何か?
ところで、「位相」とは何のことでしょうか。複素数$z=a+bi$($a,b$は実数、$i$は虚数単位)を図1.5のように複素平面にプロットしたとき、$\theta$を$z$の位相(phase)と呼びます。

▲図1.5:位相の概念
$\Ket{1}$の係数の符号を反転(-1倍)すると図1.6のように位相が半周変化するため、位相反転と呼ばれます。

▲図1.6:位相反転
■”ゲートがない”状態を作る
単位行列はもっとも基本的な量子ゲートです。
$I := \TwoTwo{1}{0}{0}{1}$
単位行列$I$がユニタリ行列であることの確認は省略しますが、実際に確認してみてください。
下記の計算例からも明らかなように、単位行列ですので、元のままですね。元のままなので使い道がなさそうな気もしますが、複数の量子ビットを扱うときに「特定の量子ビットを変化させないゲート」として活躍します。量子回路を書くときは、図1.7のように表記します。

▲図1.7:単位行列の量子回路
$I$により、量子状態$\Ket{0}, \Ket{1}, \Superposition, \SuperpositionZ$は次のように変化します。
■エルミート行列の性質
今回で紹介したユニタリ行列はいずれも随伴行列(忘れた方は第2話を確認してください)が自分自身に一致します。
$\begin{array}{l} U^{\dagger}=U \end{array}$
このような行列をエルミート行列(Hermitian matrix)といいます。
$\begin{array}{l} I^{\dagger}=I, \quad X^{\dagger}=X, \quad Z^{\dagger}=Z, \quad H^{\dagger}=H \end{array}$
そのため、自分自身が逆行列になります。また、2乗すると$I$になります。
このことから、任意の量子状態$\Ket{x}$に対して、次が成り立ちます。
このように$I, X, Z, H$は「2回ユニタリ発展させると元に戻る」という性質があります。
■量子ビットを測定する
第2回でも説明したように、量子状態を測定することで計算結果を得ます。そのため、計算した後は基本的に測定を行うことになります。また、測定前の量子状態が何であっても、測定後の量子状態は$\Ket{0}$か$\Ket{1}$になることに注意が必要です。
量子回路を書くときは、図1.8のように表記します。

▲図1.8:測定を表現する量子回路
この回路の上側の線は、量子ビットを表します。この回路の下側の二重線は、古典ビットを表します。量子ビットを測定し、測定値を古典ビットにコピーします。
1量子ビットの量子回路を行列で表現する
ここまで説明した内容を使い、量子回路の記法を説明します。たとえば、
- 量子ビットの初期値を$\Ket{0}$とする。
- パウリ行列$X$でビット反転させる。
- アダマール行列$H$で重ね合わせ状態を作る。
- 測定する。
という計算を行う量子回路は、図1.9のように表記します。

▲図1.9:量子回路の例
見た目の雰囲気は古典回路に似ていますが、量子ビットと古典ビットの線があったりと、違いがあります。 左側の$\Ket{0}$は量子ビットの初期状態、$0$は古典ビットの初期状態です。
$HX\Ket{0}$を測定して$\Ket{0}$を得る確率は$\left|\frac{1}{\sqrt{2}}\right|^2 = \frac{1}{2}$、$\Ket{1}$を得る確率は$\left|\frac{-1}{\sqrt{2}}\right|^2 = \frac{1}{2}$となります。
量子回路は左から右に進みますが、対応するユニタリ行列の積は右から左に並べるので注意してください。
2量子ビットの計算
2古典ビットは00, 01, 10, 11のように、1古典ビットを並べて書きます。これに対応する2量子ビットは$\Ket{0}\otimes\Ket{0}, \Ket{0}\otimes\Ket{1}, \Ket{1}\otimes\Ket{0}, \Ket{1}\otimes\Ket{1}$のように行列のテンソル積$\otimes$を使って表します。
ベクトルのテンソル積は次のように計算します。
$2 \times 1$行列と$2 \times 1$行列のテンソル積であるため、$4 \times 1$行列となります。そのため、2量子ビットの量子状態は4次元のベクトルになます。
$\Ket{0}\otimes\Ket{0}$はゼロベクトルでない点に注意してください。
$\Ket{0}\otimes\Ket{0} \neq \FourOne{0}{0}{0}{0}$
また、テンソル積の記号$\otimes$を省略して$\Ket{0}\Ket{0}$と表したり、さらに省略して$\Ket{00}$と表すことも多いです。
$\Ket{0}\otimes\Ket{0} = \Ket{0}\Ket{0} = \Ket{00}$
この記法を利用することで、
$\begin{array}{ll} \FourOne{a}{b}{c}{d} & = a\FourOne{1}{0}{0}{0} + b\FourOne{0}{1}{0}{0} + c\FourOne{0}{0}{1}{0} + d\FourOne{0}{0}{0}{1}\\[10pt] & = a\Ket{00} + b\Ket{01} + c\Ket{10} + d\Ket{11} \end{array}$
と書けます。
2量子ビットの量子状態は次のように定義します。

この定義は「複素数を成分とした2次元のベクトルで$|a|^2 + |b|^2 + |c|^2 + |d|^2 = 1$を満たすもの」という意味です。$|a|$や$|b|$は複素数の絶対値を表します。複素数が難しいと感じる方は、実数の絶対値(符号をプラスにしたもの)をイメージしてください。
また、2量子ビットのユニタリ発展は次のようになります。

たとえば、 ユニタリ行列$\XtensorZ$で量子状態$\FourOne{1}{0}{0}{0}$をユニタリ発展させると、
となり、これもまた量子状態になります(これらが本当に量子状態やユニタリ行列の定義を満たすことを確認してみましょう)。
2量子ビットの測定も、1量子ビットと同じように定義します。

たとえば、
とし、$\Ket{\varphi}$を測定すると、量子ビット$\Ket{00}$を得る確率は$\left|\frac{1}{\sqrt{5}}\right|^2 = \frac{1}{5}$となり、量子ビット$\Ket{11}$を得る確率は$\left|\frac{2}{\sqrt{5}}\right|^2 = \frac{4}{5}$となります。
標的ビットを制御する「CNOT」ゲート
代表的な2量子ビットの量子ゲートであるCNOTゲート(Controlled NOT gete, シーノットゲート)を紹介します。
$\CNOT := \CNOTmatrix$
証明は書きませんが、この行列が本当にユニタリ行列であることを確認してみてください。
また、$\CNOT$は4文字のひとかたまりで、1つの行列を表します。 $\rm{C \cdot N \cdot O \cdot T}$のようにバラバラにしないでください。
$\CNOT$ゲートにより、量子状態$\Ket{0}\otimes\Ket{0}, \Ket{0}\otimes\Ket{1}, \Ket{1}\otimes\Ket{0}, \Ket{1}\otimes\Ket{1}$の変化が気になる人は詳しく見てみてください。
0番目の量子ビットが$\Ket{0}$のときは、入力された量子状態を出力します。また、0番目の量子ビットが$\Ket{1}$のときは、1番目の量子ビットをビット反転させます。
そのため、0番目の量子ビットを制御ビット(control bit)といい、1番目の量子ビットを標的ビット(target bit)といいます。
「制御ビット、標的ビット」の順に添え字を明記して、$\CNOT$とも書きます。
量子回路を書くときは、図1.10のように表記します。「$\bullet$」が制御ビット、「$\oplus$」が標的ビットです。

▲図1.10:CNOTゲートの量子回路
制御ビットと標的ビットの動きを量子回路で可視化すると、次のようになります。

▲図1.11:CNOTゲートの動作: 制御ビットが|0⟩の場合は、何も変化しない

▲図1.12:CNOTゲートの動作: 制御ビットが|1⟩の場合は、標的ビットを反転する
2量子ビットの量子回路を行列で表現する
最後に、ここまで説明した内容を使い、簡単な2量子ビットの量子回路の回路図で表してみましょう。たとえば、
- 量子ビットの初期値を$\Ket{0}\otimes\Ket{0}$とする。
- アダマール行列
$H$を0番目の量子ビットに適用する。 - 0番目の量子ビットを制御ビット、1番目の量子ビットを標的ビットにした$\CNOT$ゲートを適用する。
- 測定する。
という計算を行う量子回路は、図1.13のように表記します。
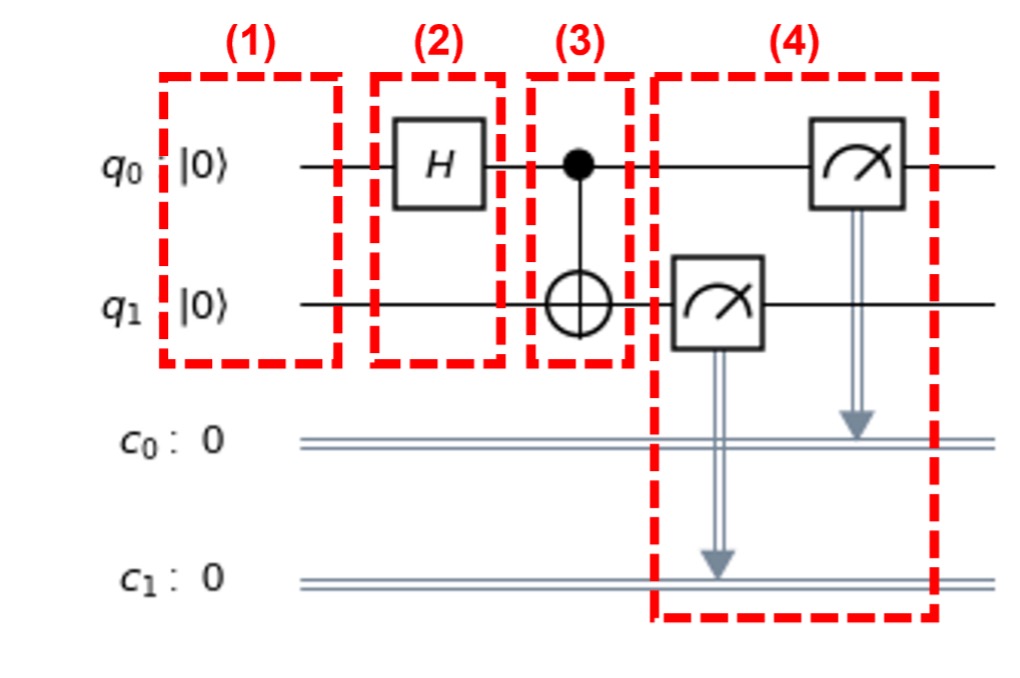
▲図1.13:2量子ビットの量子回路の例
行列を使って表すと、次のようになります。
量子回路は左から右に進みますが、対応するユニタリ行列の積は右から左に並べるため、注意してください。 $\CNOT \cdot H_0(\Ket{0}\otimes\Ket{0})$を測定して$\Ket{0}\Ket{0}$を得る確率は$\left|\FracTwo\right|^2 = \frac{1}{2}$、$\Ket{1}\Ket{1}$を得る確率は$\left|\FracTwo\right|^2 = \frac{1}{2}$となります。
量子ビットが多くなっても、1量子ビットまたは2量子ビットのユニタリ発展の組み合わせで表現できるケースも多いです。さまざまな量子回路を書き、このような計算経験を積み重ねることで、より大きな量子状態の変化が分かるようになります。
今回はここまでとなります。2量子ビットのあたりは少し複雑度が増しています。1度で分からなかったとしても、復習して理解しましょう。次回はPythonを使い、いよいよ量子プログラミングを行います。
(コラム)意外と知られていない量子コンピュータを支える技術
量子アルゴリズムや量子ビットの物理実装は、注目を浴びている重要な要素です。これらを古典コンピュータの要素と対応付けると次のようになります。

一方で、実際に古典コンピュータを実現している要素は、アルゴリズムやCPUだけではありません。ソフトウェア技術でいえばプログラミング言語やコンパイラ等がありますし、ハードウェア技術でいえばメモリやハードディスク等があります。また、コンピュータ同士で通信を行うネットワーク技術もあります。実用的なコンピュータは、多くの要素に支えられている複雑なシステムです。
もちろん、量子コンピュータを実現する場合も、量子アルゴリズムと量子ビットの物理実装だけでなく、さまざまな要素が必要です。そこで今回から数回に分けて、一般にはあまり知られていない、量子コンピュータを支える技術をいくつか紹介します。
■量子コンピュータの実行結果を検証する技術 - 量子状態トモグラフィ
この連載の先の回で、量子コンピュータの実機に対して命令を実行します。そこで実感できると思いますが、量子コンピュータの実機にはノイズがあるため、理想値と誤差があります。

▲図1.9:量子回路の例
たとえば、先程も登場した(図1.9)の量子回路を測定した場合、$\Ket{0}$と$\Ket{1}$を得る確率はそれぞれ$\frac{1}{2}$です。しかし、実際に実行してみると、$\frac{1}{2}$から数%ずれます。
量子コンピュータを開発する側としては、できる限り理想値に近い状態になるようチューニングにしたいです。そのためには、量子回路で作った量子状態$a \Ket{0} + b\Ket{1}$のパラメータ(この場合は$a$と$b$)を具体的に推定し、実行結果を検証する必要があります。基本的には「量子状態を作成し、測定する」ということを何度も繰り返し、測定結果から量子状態を推定します(図 1.14)。
このように、量子状態を推定する技術を量子状態トモグラフィ(quantum state tomography)といいます。量子状態トモグラフィにはさまざまな手法がありますが、ここではシンプルな手法を紹介します。

▲ 図 1.14: 量子状態トモグラフィ
量子状態$a\Ket{0} +b\Ket{1}$の$a$と$b$の具体的な値が分かっていないとします。この量子状態を測定したとき、$\Ket{0}$を得る確率は$|a|^2$、$\Ket{1}$を得る確率は$|b|^2$となります。「量子状態を作成し、測定する」を何度も繰り返して$\Ket{0}$や$\Ket{1}$を得る確率を調べれば$|a|^2$と$|b|^2$を推定できます。
統計学を用いると、推定精度を$ε$程度にするには、$\frac{1}{ε^2}$回の測定が必要になることが分かります。たとえば、小数第1位まで推定する場合は$ε= 0.1 = 1/10 なので10^2=100$回、小数第2位まで推定する場合は$ε= 0.01 = 1/100$なので$100^2=10000$回の測定が必要です。
ただし、このままだとシンプルすぎて$\Superposition, \SuperpositionZ$のような量子状態を区別できません。なぜかというと、どちらの量子状態を測定しても$\Ket{0}$を得る確率が$\frac{1}{2}$になるため、単に測定するだけでは区別できないためです。
そこで、このような量子状態も区別できるよう、測定に工夫が必要になります。工夫の具体的な内容は省きますが、これにより測定回数が3倍になります(図 1.15)。

▲ 図 1.15: 測定の工夫により、量子状態を区別
最終的に複素数$a$と$b$を小数第2位まで推定するには、30,000回の測定が必要になります。人間が計算すると大変ですが、コンピュータならそれほど時間はかかりません。この方法によって、目的の量子状態をどの程度正しく作成できたか推定でき、量子コンピュータの実行結果を検証できます。
実は、このシンプルな推定方法には問題があります。量子ビット数が増加すると推定に必要な測定回数が指数関数的に増加するため、コンピュータで推定するのも大変になるのです。一方で、実用的な量子コンピュータに向けて量子ビット数を大幅に増やしても、正しく動作しているか検証できる必要があります。そのため、実行結果の検証は量子コンピュータに欠かせない技術であり、効率的に検証するさまざまな手法が研究されています。
▼これまでの「初心者でもわかる量子コンピュータの計算の仕組み」
【第1話】数式なしで量子コンピュータの現状を理解しよう
【第2話】量子コンピュータで使用する計算の土台を学ぼう
【第3話】量子コンピュータの基本のルールを学ぼう
【第4話】基本の量子ゲートと量子回路をおさえよう
【第5話】量子プログラミングをやってみよう
【最終話】現在の量子コンピュータの限界とこれから
束野仁政さんの著書『量子コンピュータの頭の中――計算しながら理解する量子アルゴリズムの世界(技術評論社)』もあわせてご覧ください。(2023年7月追記)


