思考力を試す、ナゾ解き!出題者は、アルゴリズムの書籍や競技プログラミングの解説記事を多数執筆する大槻兼資さんです。今回の題材は「石取りゲーム」。
「難しい問題に挑戦したい」といったご感想を多くいただきました。そこで今回は、難易度90(!)の問題をご用意。ゲームAIの世界の一端に触れ、その面白さを感じてみませんか?
本連載では、実際に社会の中で役に立っている数学を題材として、簡単なクイズを出題していきます。読者の中には、中学校や高校で数学の学習に苦しんだ方もいるかもしれません。「こんなことを学んで何の役に立つのだろうか?」と感じた方も多いかもしれません。しかしながら、数学は私たちの暮らす社会の中で、さまざまに使われています。学生時代に数学が苦手だった方も、ぜひ肩の力を抜いて、挑戦してみてください! 大槻兼資
問題
30個の石からなる山があります。
太郎君と花子さんは、太郎君を先手として、交互に次のいずれかの操作を行います。
- 山から2個の石を取り除く(ただし、山の石が2個未満の場合はこの操作はできません)
- 山から3個の石を取り除く(ただし、山の石が3個未満の場合はこの操作はできません)
先に石を取れなくなった方が負けです。太郎君と花子さんが最善を尽くした場合、どちらが勝つでしょうか?
ぜひ、家族や友人と一緒に遊んでみてください!
例題(ヒント)
最初の石の山に含まれる石の個数が7個の場合を考えてみましょう。この場合は、太郎君と花子さんのどちらが勝てるでしょうか?
結論から述べると、太郎君の勝ち(先手必勝)です。
太郎君は最初に2個の石を取り除き、山に残る石の個数を5個にすればよいのです。
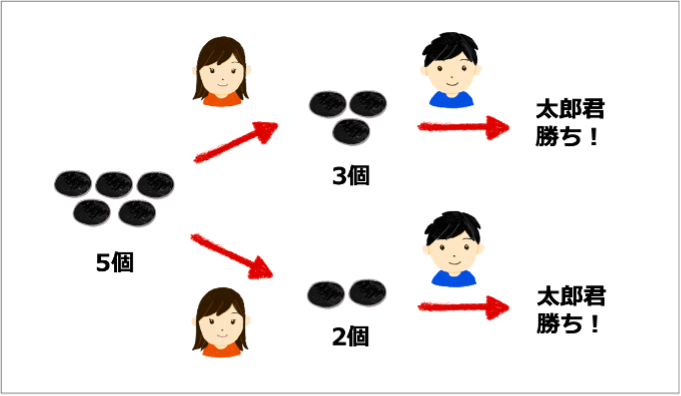
このあと、花子さんが2個の石を取った場合も、3個の石を取った場合も、いずれも太郎君が勝つことができます。より詳しく述べると、
- 花子さんが2個の石を取った場合:山に残る石の個数が3個になります。このとき、太郎君は残り3個の石をすべて取り除くことで勝つことができます。
- 花子さんが3個の石を取った場合:山に残る石の個数が2個になります。このとき、太郎君は残り2個の石をすべて取り除くことで勝つことができます。
アドバンスト
「最初の石が30個の場合」が難なく解けたという方は、この問題を一般化してみてください。つまり、
- 最初の石の山に含まれる石の個数をN個とする
- 各ターンでプレイヤーが取れる石の個数をA個またはB個とする
という石取りゲームを考えます。
この一般化した石取りゲームで、コンピュータを活用して、N, A, B の値が100000程度であっても、先手必勝か後手必勝かを求めることのできる方法を考えてみてください。
クイズの応用例
このナゾ解きは、「ゲームを解く」ことを問うものです。そして、その考え方は、より複雑なゲーム......たとえば、オセロ、将棋、囲碁などの解析にも繋がるものです。
ゲームを解くとは、先手必勝であるか後手必勝であるかを特定したり、必勝手順を求めたりすることをいいます*。代表的なゲームとしては、オセロや将棋などがあります。最近は、オセロは双方最善を尽くすと引き分けになることが証明された、という衝撃的なニュースもありましたね。オセロはついに陥落してしまいましたが、将棋や囲碁については、解かれるのはまだ先のことになりそうです。
* ここでいうゲームは、二人プレイのものであって、協力プレイの形式のものではなく、有限回の手順で必ず勝敗が決まり、確率要素がなく、隠された情報がないものを考えています。このようなゲームを二人零和有限確定完全情報ゲームといいます。
二人零和有限確定完全情報ゲームにおいて、ゲームの初期盤面で勝敗のみがわかることを超弱解決、初期盤面で勝敗がわかっていてそれを証明するのに必要な各局面の最善手もわかることを弱解決、すべての局面について勝敗も最善手もわかることを強解決と呼んで区別することもあります。解答
それでは、正解を発表します。
・
・
・
「最初の石が30個の場合」の勝者は、花子さん(後手必勝)です。
みなさんは正答できたでしょうか。できた方は、なぜこの方法が最適なのか、その理由まで考えてみましょう。
解説
それでは、解説を始めます。少し難しいかもしれませんが、具体的な例に対して手を動かすなどして、少しでも感覚をつかんでみてください。
石の個数がN個の状態で手番となった者が勝てるとき、「石の個数がN個の状態は勝ちである」ということにします。逆に、石の個数がN個の状態で手番となった者が負けるとき、「石の個数がN個の状態は負けである」ということにします。
つまり、石の個数がN個の状態が勝ちであるということは、石の個数がN個の状態でゲームを始めると先手必勝であるということです。
N = 0,1,2,3,4 の場合について、石の個数がN個の状態の勝ち負けを整理すると、下の表のようになります。

さて、N = 5 の場合は勝ちでしょうか?負けでしょうか?これは、先ほどの例題で結論を出していますね。
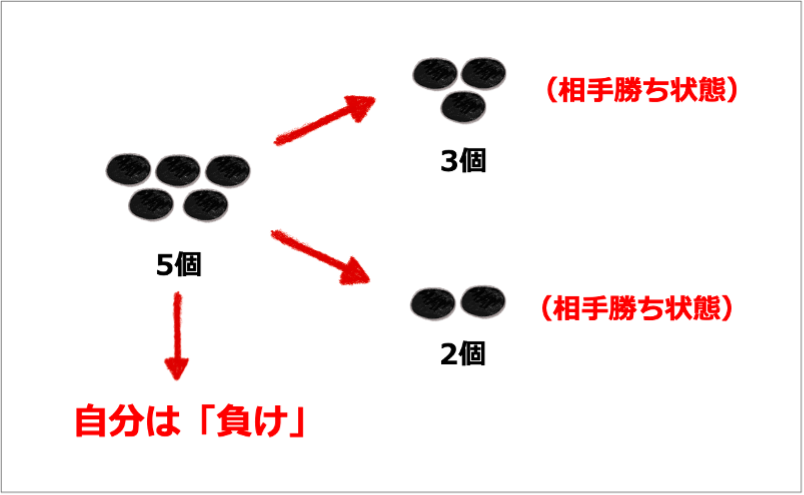
- 石を2個とるとき:残りの石の個数は3個であり、この状態は「勝ち」である。つまり、相手に「勝ち」を渡すことになります
- 石を3個とるとき:残りの石の個数は2個であり、この状態は「勝ち」である。つまり、相手に「勝ち」を渡すことになります
石を2個とっても、3個とっても、結局相手が勝つのです。つまり、石が5個の状態は「負け」であるということです。
一般に、石の個数が N (≧ 3) 個の状態の勝ち負けについては、次のように考えればよいでしょう。
- 石の個数が N - 2 個の状態と N - 3 個の状態がともに「勝ち」であるとき、石の個数がN個の状態は「負け」である
- 石の個数が N - 2 個の状態と N - 3 個の状態のいずれかが「負け」であるとき、石の個数がN個の状態は「勝ち」である
この考え方にしたがって、N = 6, 7, ... の場合についても勝ち負けを求めると、次のようになります。
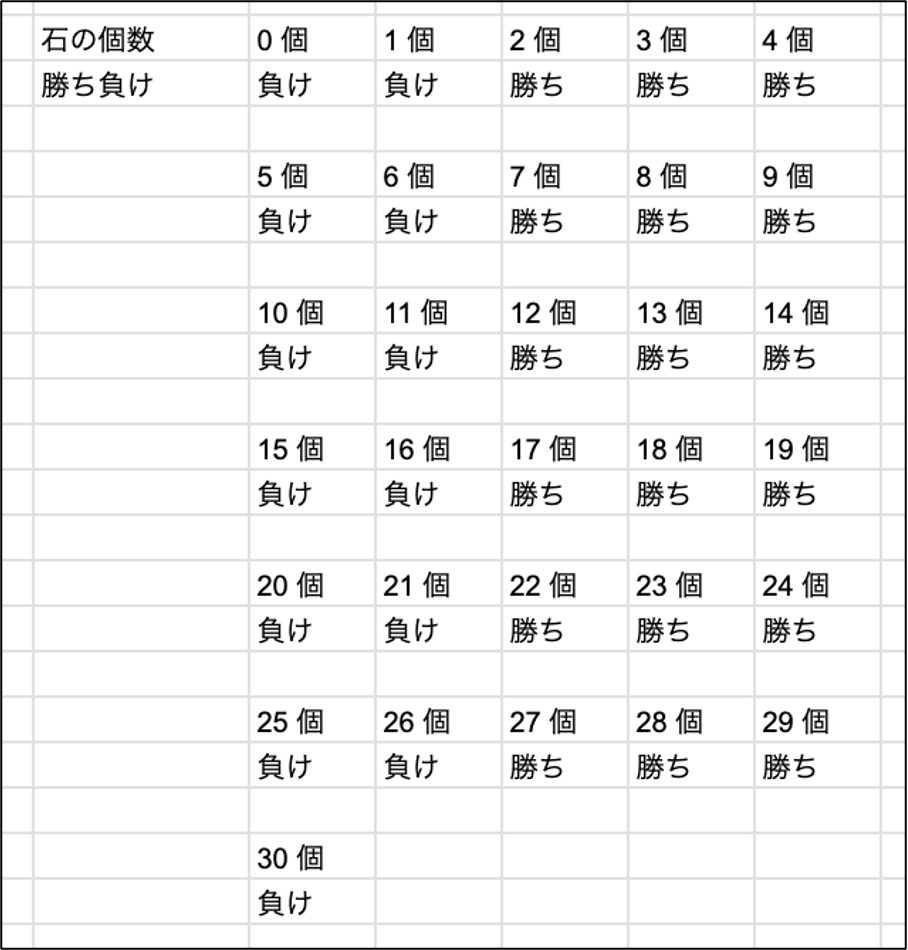
したがって、石が30個の状態は「負け」であり、石が30個の状態でゲームをスタートすると花子さんの勝ち(後手必勝)であることがわかりました。
補足
上の表をみると、次の規則性が読み取れます。
- 石の個数を5で割った余りが0,1の状態:「負け」である
- 石の個数を5で割った余りが2,3,4の状態:「勝ち」である
おわりに
最後に、このクイズの解法と数学との関連を紹介します。
今回のゲームの勝敗を求めた方法は、次のような「漸化式」を立てて解いたものとみなすことができます。漸化式は、数学Bの単元「数列」で登場するものですね。

第1回(カーナビ)、第2回(diffコマンド)も、広く捉えると「漸化式」を立てて解いたものとみなすことができます。ぜひ、あわせて考えてみてください。
アドバンス問題の解答
以下に示すプログラムは、石の個数が100000個の場合でも、コンピュータを活用して解くことのできるものです。C++で記述しています。
#include <iostream>
#include <vector>
using namespace std;
int main() {
// N: 山の石の個数
// A, B: プレイ時に取れる石の個数
int N, A, B;
cin >> N >> A >> B;
// is_win[i]: 山の石の個数が i 個のときに、勝てるかどうか
vector<bool> is_win(N + 1, false); // 「負け」で初期化しておく
// i = 1, 2, 3, ..., N 個の場合に勝てるかどうかを順に求める
for (int i = 1; i <= N; i++) {
// A 個取る場合を試す(A 個とった状態が負けならば、現在の状態は勝ち)
if (i - A >= 0 && !is_win[i - A]) is_win[i] = true;
// B 個取る場合を試す(B 個とった状態が負けならば、現在の状態は勝ち)
if (i - B >= 0 && !is_win[i - B]) is_win[i] = true;
}
// 石の山の個数が 1, 2, ..., N の場合に勝ちかどうかを出力する
for (int i = 1; i <= N; i++) {
cout << "石の個数が " << i << " 個のとき: " << (is_win[i] ? "勝ち" : "負け") << endl;
}
}
```
たとえば、
```
30 2 3
```
を入力すると、次のように出力されます。
```
石の個数が 1 個のとき: 負け
石の個数が 2 個のとき: 勝ち
石の個数が 3 個のとき: 勝ち
石の個数が 4 個のとき: 勝ち
石の個数が 5 個のとき: 負け
石の個数が 6 個のとき: 負け
石の個数が 7 個のとき: 勝ち
石の個数が 8 個のとき: 勝ち
石の個数が 9 個のとき: 勝ち
石の個数が 10 個のとき: 負け
石の個数が 11 個のとき: 負け
石の個数が 12 個のとき: 勝ち
石の個数が 13 個のとき: 勝ち
石の個数が 14 個のとき: 勝ち
石の個数が 15 個のとき: 負け
石の個数が 16 個のとき: 負け
石の個数が 17 個のとき: 勝ち
石の個数が 18 個のとき: 勝ち
石の個数が 19 個のとき: 勝ち
石の個数が 20 個のとき: 負け
石の個数が 21 個のとき: 負け
石の個数が 22 個のとき: 勝ち
石の個数が 23 個のとき: 勝ち
石の個数が 24 個のとき: 勝ち
石の個数が 25 個のとき: 負け
石の個数が 26 個のとき: 負け
石の個数が 27 個のとき: 勝ち
石の個数が 28 個のとき: 勝ち
石の個数が 29 個のとき: 勝ち
石の個数が 30 個のとき: 負け
▼これまでの謎解きにも挑戦!
・【ナゾ解き】現在地から目的地に辿り着くまでの最短経路は?
・【ナゾ解き】2つの文字列は、どのくらい離れている?(diff コマンド)
筆者・出題者:大槻 兼資さん
株式会社NTTデータ数理システム顧問、モノグサ株式会社コンテンツアーキテクト。数学や情報科学の諸分野の教材開発や啓蒙活動に従事。「けんちょん」の愛称で親しまれている。著書に『問題解決力を鍛える!アルゴリズムとデータ構造』(講談社)がある。数理最適化や機械学習を活用した数理コンサルティング業務の経験も多数。趣味は競技プログラミング、虫食算作り、国内旅行など。
ファクトチェック:増井 敏克さん
増井技術士事務所代表。技術士(情報工学部門)。情報処理技術者試験にも多数合格。ビジネス数学検定1級。「ビジネス」×「数学」×「IT」を組み合わせ、コンピュータを「正しく」「効率よく」使うためのスキルアップ支援や、各種ソフトウェアの開発、データ分析などを行う。著書は『プログラマ脳を鍛える数学パズル シンプルで高速なコードが書けるようになる70問』『プログラマを育てる脳トレパズル 遊んでおぼえるPythonプログラミング&アルゴリズム』(翔泳社)など多数。